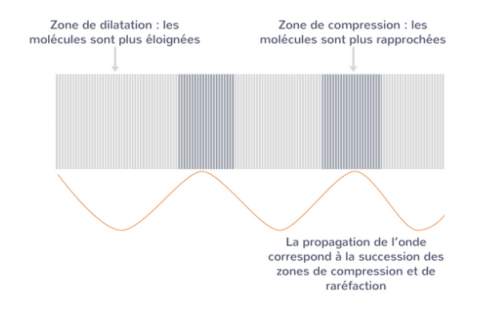
Décrire ce qui se passe lorsque l'on utilise un diapason et sa caisse de résonance pour émettre un son et la propagation de ce sont dans l'air.
Vous pouvez utiliser le schéma ci-dessous.
Préciser l'intérêt de la caisse de résonance du diapason.
.
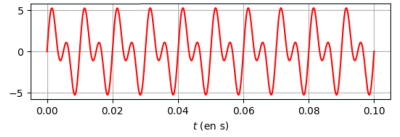
L'enregistrement ci-contre correspond à celui d'un son : en abscisse on trouve le temps (en seconde) et en ordonnée la valeur de la tension (en volt) qui correspond ici à l'intensité du signal.
2. Pourquoi peut-on affirmer que ce son est « périodique » ?
3. Définir la période notée « T » d'un signal sonore.
4. Déterminer la période de ce signal sonore à partir de l'enregistrement ci-contre. Pour une mesure précise, vous devez prendre en compte le maximum de périodes.
5. La fréquence d'un signal sonore est le nombre de période qui s'écoulent en une seconde. Utiliser cette définition de la fréquence pour déterminer la fréquence de ce signal sonore.
Pour calculer la fréquence « f » d'un son lorsque l'on connait sa période « T » on peut utiliser la relation suivante :
T x f = 1
la fréquence doit être exprimée en Hertz (Hz)
la période doit être exprimée en seconde (s)
.
6.1. Observer les deux enregistrements sonores ci-dessous. Pourquoi peut-on qualifier l'un de ces sons de son « pur » et l'autre de son « complexe » ?
6.2. Déterminer la période du son B.
 |  |
Méthode :
Installe l'application gratuite FIZZIQ sur votre smartphone (pour Androïd et pour Iphone).
Ouvre cette application. Dans l'onglet « outils », sélectionne dans la « bibliothèque de sons » le fichier « diapason La3 » puis lance l'exécution de ce son. Il va se jouer indéfiniment jusqu'à ce que tu arrêtes leur exécution.
En parallèle, va dans l'onglet « mesures », puis sélectionne le capteur « microphone », puis « Fréquence fondamentale » : cet outil va te permettre d'enregistrer et de déterminer la fréquence de la note qui est jouée.
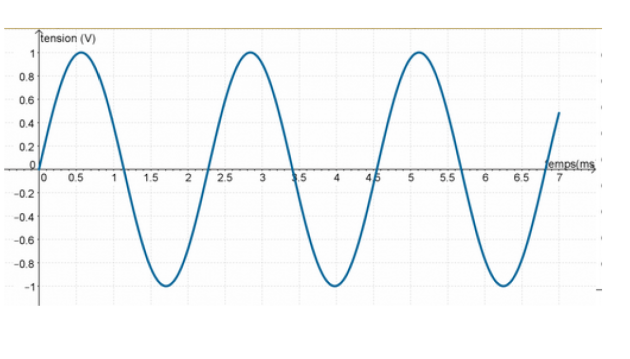
7. Relève la fréquence de ce son.
8. De nouveau dans l'onglet « mesures », « microphone », puis « amplitude » : décris l'oscillogramme obtenu pour ce son. Peut-on le qualifier de « son complexe » ?
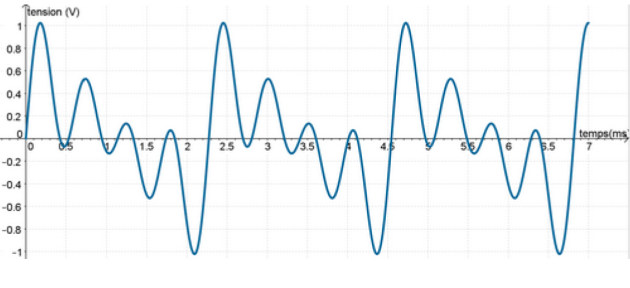
Tu vas recommencer les mêmes manipulations mais avec le fichier son correspondant au « piano 1 ».
9. Détermine la fréquence de ce son. Est-ce un son complexe ? Justifie ta réponse.
.
Complément : analyse spectrale
L’idée d’analyse spectrale fut imaginée par Joseph Fourier (1768-1830) : il postula en 1807 qu’un signal périodique peut s’écrire comme une somme de sinusoïdes.
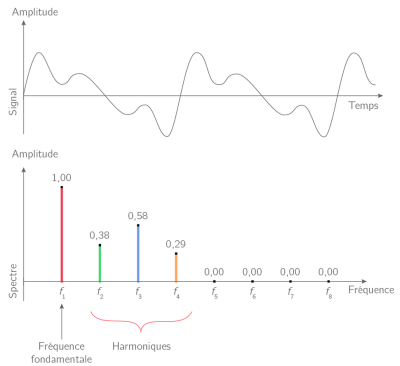
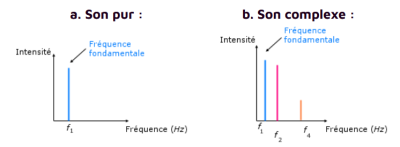
L’analyse spectrale d’un signal consiste à trouver toutes les sinusoïdes qui contribuent significativement au signal : cela veut dire identifier les fréquences et les amplitudes des sinusoïdes associées. Un spectre de Fourier, ou spectre en fréquence, est une représentation graphique permettant de visualiser ces deux grandeurs, où les fréquences sont en abscisses et les amplitudes en ordonnées.
Avec un signal périodique, le spectre se présente sous la forme de pics, situés au niveau de chaque fréquence intervenant dans le signal. Plus une fréquence contribue, plus le pic est haut, c'est-à-dire plus l’amplitude de la sinusoïde associée est forte.
Le spectre de fréquence d’un son pur (ou son simple) n’est composé que d’un seul pic qui correspond à la fréquence fondamentale.
Le spectre de fréquence d’un son complexe est composé de plusieurs pics : la fréquence la plus faible correspond à la fréquence fondamentale, les autres composantes aux harmoniques.
Les fréquences des harmoniques sont des multiples de la fréquence fondamentale.
Si la fréquence fondamentale est f1 = 440 Hz, on peut obtenir des harmoniques pour les fréquences suivantes : f2 = 2 x f1 = 880 Hz, f3 = 3x f1 = 1320 Hz...
Vous aller utiliser une application pour générer un son en modifiant les harmoniques présentes.
10. Manipuler cette application pour répondre aux questions suivantes :
Qu'est-ce qui caractérise un son aigu ou un son grave ?
Qu'est-ce qui permet de modifier le volume sonore ?
Qu'est-ce qui est modifié lors l'on ajoute des harmoniques à la fréquence fondamentale ?
.
Méthode :
Choisir de nouveau l'application FIZZIQ pour générer un son émis avec le fichier « piano1 ».
Choisir ensuite l'outil de mesure « spectre ». enregistre le spectre obtenu dans ton cahier de laboratoire de l'application.
11. Déterminer les valeurs de la fréquence fondamentale de ce son et de ses harmoniques.
12. Refaire la même chose avec le fichier « piano 2 ».